概率论与数理统计公式大全(概率论与数理统计理论中值得注意的几个问题)
(1)概率论的基本概念


随机事件、样本空间:比如两个人谈恋爱,有成功和失败的两种可能,也就是随机事件包括两个:成功、失败,或者还有第三种:最后没结婚但却一直保持良好关系?如果没有,样本空间就是{成功、失败};如果有,那样本空间就是{成功、失败,没结婚却保持良好关系},也就是说,随机试验的结果称为随机事件,一个随机事件的所有的可能结果构成了样本空间。至于谈恋爱算不算随机试验,我们这里就不探讨了。
条件概率:
条件概率P(A|B)是一种定义,它表示的意思是在事件A发生的条件下事件B发生的概率,
而 P(AB)的意思是A、B两个事件同时发生。
全概率公式:

贝叶斯公式:

这两者的区别就在于原因和结果颠倒了,而之所以可以颠倒的原因就在于P(AB)=P(BA),导致:

(2)一维随机变量及其分布
这一章的关键就是正态分布曲线:

对于曲线上的每一点(x,y),其横坐标代表的数值,纵坐标代表的是比例,比如,这条曲线如果表示一个100人的班级的考试成绩,那么横坐标就是分数,纵坐标就是这个分数的学生所占比例。这条曲线从左到右所包围的面积,就是某个分数段(比如0-60)分的学生所占的比例。这条曲线的最高点就是这个班的平均分。这条曲线还表示了一个意思,就是平均分旁边的分数的学生所在比例更高,往两边比例逐渐缩小。
(3)二维随机变量及其分布
这一章的重点应该把握边缘概率密度的概念。
一维概率密度函数f(x)指的是在x固定的情况下,x的这个值的取值频度。
同样,边缘概率密度也是一样的意思:

前者是指x固定,y在整个定义域内变动,后者则反过来。
(4)随机变量的数字特征
这一章的数学期望很简单,就是样本容量N趋于无穷大时平均值的极限值。
方差按照其公式

它表示的就是所考察的全部随机数与其平均值的偏差的一种度量。
比如,两个班的学生的平均身高都是165,其中一个班的学生大多数在165附近,那么这个班的学生的身高的方差就比较小;另一个班的学生有一部分180以上,另外一部分150以下,那么这个班的方差就大。同样,如果一个国家的平均国民收入数据的方差比较大,意味着贫富差距比较大,那么,这个国家肯定在某个方面存在问题。
还有一个就是相关系数的概念,其定义
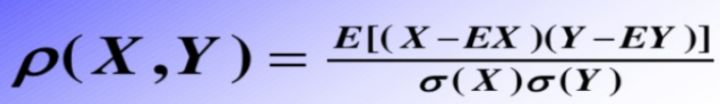
比如:


上图是完全线性相关,下图是X其中的一个点违反了规则,导致相关系数下降。那么,这个规则是什么呢?
就是被考察的两个变量,
当它们同时大于或者小于其平均值的时候
(X的均值为6,Y是12),
它们的相关系数就大,反之则小。
那么,相关系数的含义就应该是,对于两个变量其围绕它们的均值进行变化的趋势是否一致的程度的一种度量。
(5)大数定律与中心极限定理
这章的重点应该是中心极限定理。

分子分母都除以n之后,定理变成:

我们注意到,这里的变量已经变成了
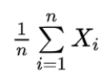
也就是说,中心极限定理说的其实是,当一组独立同分布的随机变量的数量足够大的时候, 它们的均值也服从正态分布。
2.基础数理统计
(1)抽样分布
这一章主要是理解卡方分布:

那就是把卡方统计量看作是Y=Y1+Y2+……,其中Yi=Xi^2,而Y的密度函数经过复合函数计算后为:
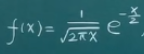
(2)参数估计和假设检验
这一章重点搞清楚似然估计和假设检验就差不多了。
似然估计:
我们常说的概率,是在已经知道随机变量某个值出现的可能性大小的情况下,来推测在某次试验中这个值会出现多少次。比如预先知道,一枚正常的硬币,在抛掷的时候,正反两面出现的可能性(概率)都是1/2,那么,如果抛掷100次,可以预测正反两面出现的次数都大概是50次;而
似然性
则是用于在已知抛掷100次硬币正反两面出现的次数的基础上,反过来推测正反两面出现的可能性(概率),即根据某些观测所得到的结果,对有关事物的性质的参数进行估计。
但是,我们应该得到一个更大的概率值,所以我们尝试了所有θ可取的值,使得表达式θ⁷ (1-θ)³取得最大值的θ为0.7左右,这就是似然值的含义,也就是说,在已经知道试验结果(7次正面,3次反面)的前提下,反过去推测θ值为多少(这里假设硬币正反两面出现的概率都可以不是1/2)才能使得试验结果表达式θ⁷ (1-θ)³的值达到最大。注意这一表达式使用的是乘法原理得到的结果。
清楚这个问题以后,我们就可以提出

假设检验:某机床厂加工一种零件,根据经验知道,该厂加工零件的椭圆度近似服从正态分布,其总体均值为m0=0.081mm,总体标准差为s= 0.025 。今换一种新机床进行加工,抽取n=200个零件进行检验,得到的椭圆度的均值为0.076mm。试问新机床加工零件的椭圆度的均值与以前有无显著差异?(a=0.05)
解题结果:

看到这个结果以后,还是会觉得不好理解,为什么就拒绝了假设H0呢?

这个计算结果就是告诉我们,新机床的产品(x)和老机床的总体均值之差处于上图的蓝色区域(z=-2.83)内,而上图中两边蓝色部分面积之和即a=0.05,也就是预先设定的检验水准。上述实验结果还表明,只有进一步缩小a值(比如3%),才能使得z=-2.83不包括在上面两个蓝色区间内,也就是在a更小的情况下,才能接受H0。这里的a代表显著性水平,显著性水平越低,就表示原假设越难被推翻,假设检验越保守。显著性水平越高,就表示原假设越容易被否定,假设检验越激进。也就是说,
显著性水平是留给某次实验用来推翻原假设的可能性的大小。
这就好比一个女孩子对一个男孩子说,你本来追不到我(H0),但我愿意给你5%的可能性(显著性水平,意味着这个男孩子要在下雨天为她送饭)试一下,结果男孩子真做到了,也追到了这个女孩(否定了H0);而当这个女孩子只愿意给3%的可能性(意味着这个男孩子要在下雪天为她送饭)的时候,结果就没有追到一样。
(2)线性模型(回归分析)和方差分析
回归方程:



回归方程系数的求解就是使得上图中的误差线段ei的平方和
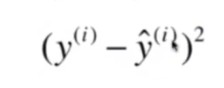
最小:

从得出的结果可以看出,所考察的每一个点都对回归方程的系数做出了贡献。
从以上的分析可以看出,数理统计这门课的知识结构大概是:先是随机变量的基本概念,然后分别在一维和二维空间对随机变量进行分析计算,然后是点估计(包括矩估计法、最大似然法、最小二乘法等来估计数学期望、方差、相关系数等),区间估计(置信区间、假设检验等)。